Post by matterbeam on May 21, 2017 18:03:34 GMT
This should be of interest to this forum. I've only included the relevant sections, the rest can be found here:
The concept
An explosive produces hot gasses that expand in all directions. A shaped charge focuses the energy of an explosive into a narrow cone. How effectively it does this is called 'directivity'.
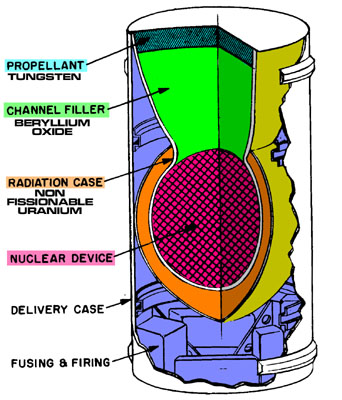
Orion nuclear pulse propulsion unit.
The energy of a shaped charge can be used to accelerate a projectile. This projectile absorbs some of the gasses' kinetic energy and some of its thermal energy.
To maximize the amount of kinetic energy gained by the projectile and to reduce how much heat it absorbs, the projectiles are made as thin sheets of metal resting on a layer of explosive filler. The filler detonates and expands in only direction - into the projectile.
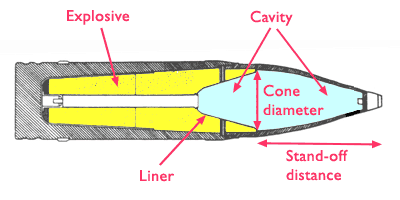
Cross-section of a HEAT warhead.
The projectile henceforth will be referred to as the 'metal plate' or the 'liner'. You can find it called the 'flyer plate' or simply 'flyer' in literature.
The angle the metal plate forms with the explosive filler determines how much of the Monroe effect it uses. At shallow angles, we produce an Explosively Formed Projectile. At sharp angles, the Monroe effect is used to pinch together the walls of the cone and squirt out a very fast jet. The latter is used today in High Explosive Anti-Tank projectiles.
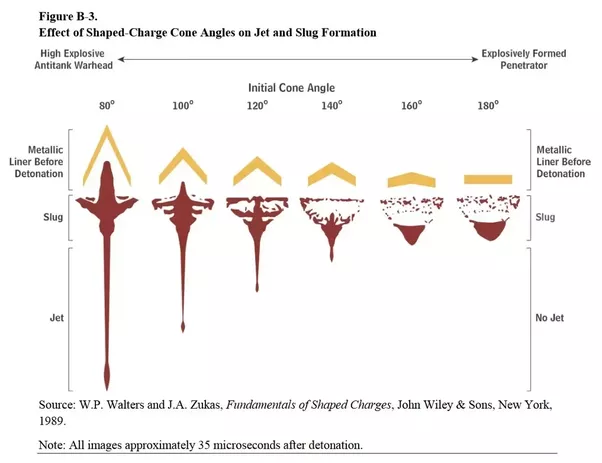
Modern weapons use chemical energy. The explosive filler is also a chemical compound, so the maximum velocity of the metal plate is proportionate to the energy density and the amount of explosive filler being used.
In this post, we will consider inert fillers being heated by nuclear shaped charges. For more information on, read the Casaba Howitzers post.
Existing performance
Chemical explosives today energy densities measured in megajoules per kg. TNT contains 4.184MJ/kg. HMX contains 6.27MJ/kg. Some chemical compounds such as some solid rocket propellants contain even higher energy densities, but do not produce the supersonic shockwave necessary in shaped charges.
These explosives create gasses reaching 3000 to 4000K. The rate of expansion of a gas, and therefore its kinetic energy, is strongly dependent on its temperature. Therefore, a hotter gas contains more energy and can accelerate a metal plate even faster.
Modern EFPs manage to propel their metal plates at velocities ranging from 2000 to 3000m/s. Attempting even higher velocities quickly requires huge amounts of explosive filler.
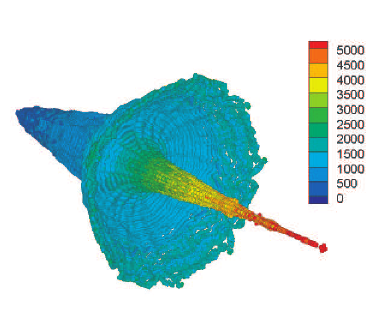
Velocity distribution in a HEAT jet. Numbers in m/s. Jet tip 5km/s, body 1500m/s, rearmost slug immobile.
HEAT weapons manage to accelerate the tip of their jets to velocities ranging from 7 to 14km/s. The remainder of the metal lining reaches much slower 1-2km/s velocities, with the deepest segment not being accelerated at all. This velocity differential stretches out the jet until it fragments into ineffective pieces, which severely limits the effective range.
Nuclear Explosive Formed Projectiles
The idea here is weaponize the nuclear pulse propulsion units designed for use in the Orion drive.
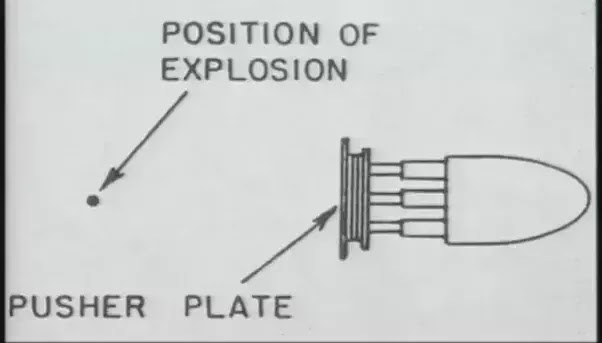
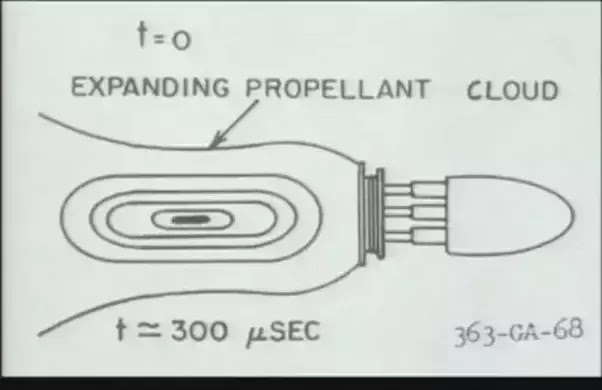
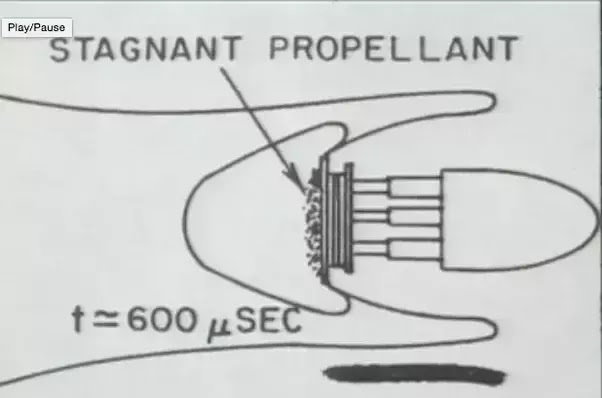
Orion pulse sequence.
From the original project, we know that 85% of the nuclear yield can be directed into a narrow cone of 22 degrees or less. Instead of allowing beryllium filler particles to fly out into space, we place a thick metal plate on top.
In a NEFP, the metal plate is at a very shallow angle.
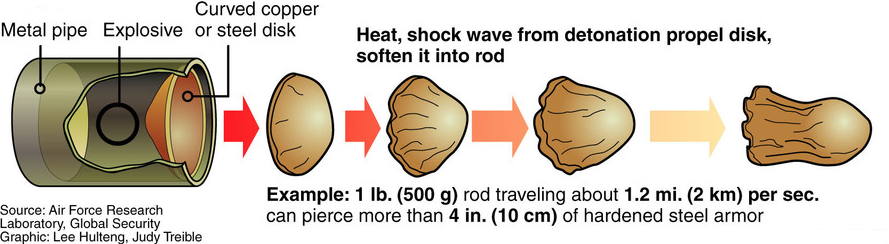
Research has already put into the concept, as published by Science and Global Security 1990.
NEFP velocity
The main requirement of a NEFP is that the energy deposited into the metal lining is not sufficient to vaporize it.
Copper's melting point is about 1400K. Refractory materials such as tungsten can stay semi-solid at 3600K. Some materials can stay solid at even higher temperatures, but would not exhibit the plastic behaviour of metals. This limits the maximum metal plate temperatures to about 3500K.
We can use the contemporary performance of Explosively Formed Penetrators to estimate the maximum temperature of the filler in a nuclear design.
This study from Thermal Science 2016 tracked the temperatures and pressures in a copper plate being driven by Octol, a mix of TNT and HMX. Octol has a detonation velocity of 2000m/s and a specific energy of 6.3MJ/kg.
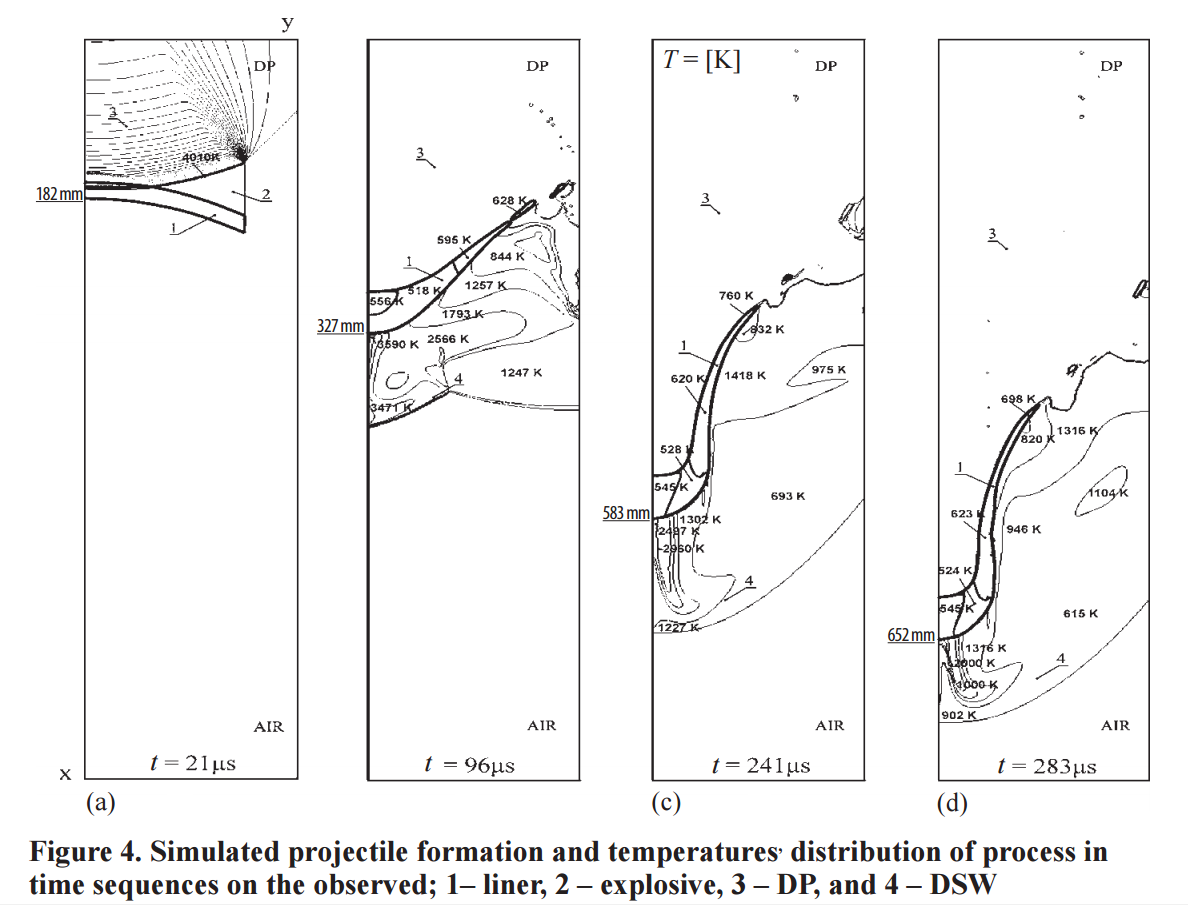
We observe that the copper reaches temperatures around 622K if we average between the 545 and 698K in the last frame.The gasses driving it reach 4010K. In the experiment, the copper is 10mm thick, masses 12.5kg and is shaped as a hemisphere 150mm in radius, for an 'exposed' area of 0.14m^2.
Copper's heat capacity is 385kJ/kg/K and its heat conductivity is 385W/mK.
Tungsten's heat capacity is 133kJ/kg/K and its heat conductivity is 100W/mK.
If we substituted copper for tungsten, the metal plate would survive 3500K, a temperature 5.83 times higher, but requires only 2.04 times more energy due to the lower heat capacity.
Heat transfer by conduction is linear with the temperature difference. In the Thermal Science test, the copper started at 300K and ended up at 622K, averaging a 3548K temperature difference between the hot gasses and the metal plate.
A tungsten plate would heat up from 300K to 3500K, averaging 1900K. Its heat conductivity is 3.85 times lower than that of copper, so the temperature difference can be allowed to become 3.85 times higher for the same heating effect.
Considering all these factors, tungsten can survive a temperature difference 3.85 * 2.04 : 7.85 times higher.
This works out to a tungsten plate would average 1900K if it is accelerated by a gas of temperature just under 30000K.
This gas contains 7.42 times more energy than high explosive gas. It would accelerate a tungsten plate to a velocity 2.7 times faster.
We can safely say that Explosively Formed Projectiles can be propelled about three times faster using nuclear energy than using chemical explosives. This suggests velocities of about 6 to 9km/s.
Higher velocities can be achieved if we accept the fragmentation of the metal plate. These fragments have a theoretical velocity of 100km/s.
Even higher velocities, such as those cited in the Science & Global Security article, are the result of explosive fillers being heated to millions of Kelvins. They allow for velocities of up to 3% of the speed of light, as fast as the particles in a Casaba Howitzer. However, heating a metal liner and an explosive filler to those temperatures turn them into a plasma, and plasma-plasma interactions do not allow for much of the nuclear weapon's yield to be converted into kinetic energy.
NEFP efficiency

Relevant section underlined in red.
According to Friedwardt Winterberg, 50% of the nuclear blast is converted into the kinetic motion of the particles in the shaped charge's explosive filler. The rest goes into heating the filler.

M the metal place, C the explosive filler.
Since the nuclear blast also destroys everything aft of the explosive filler, the configuration is assumed to be an 'open-faced sandwich'. Roughly 50% of the filler's kinetic energy is used to accelerate the metal plate in the target's direction.
Using the 85% efficiency for the nuclear blast, 50% for the filler and 50% for the metal plate, about 21% of the nuclear yield ends up in the projectile.
This is better than the 5% efficiency listed in experimental studies.
In a NEFP, this means that a 1 kiloton yield warhead could propel more than 21.7 tons of metal at the target at 9km/s.
This literal boulder would be immune to most forms of anti-missile defenses, such as Whipple shields, lasers, missile interceptors or even wide-angle defensive Casaba Howitzers.
A 2m wide 21.7 ton tungsten projectile would be 352mm thick. Using the hydrodynamic penetration model, this projectile would penetrate 947mm of aluminium. Armor materials suited to resisting laser fire would be less dense and suffer greater penetration. This isn't an exceptional penetration depth for the mass invested in the weapon.
Instead, the metal has incredible momentum. Striking a 10000 ton target would knock the target back at 19.5m/s. In practice, this would break the target in half through sheer mechanical stress. The relatively size of the projectile makes the impact resemble a cannonball ploughing through a building.
Spaced NEFP
In the Orion drive, the nuclear pulsed propulsion charges are detonated at a distance of 25 meters from the pusher plate. This spacing allows for the hot plasma (67000K) ejected by the nuclear charge to expand and cool down to 14000K. This greatly reduced the erosion and heating of the pusher plate.
USAF 10m Orion
A similar concept can be used to allow nuclear EFPs to both use high-temperature gasses and the high kinetic efficiency of solid metal plates.
By spacing the explosive filler from the metal plate, an initially very hot plasma can be accelerate a solid plate without vaporising the latter.
The advantage is that a very hot plasma allows for very fast EFPs and much lighter weapons. The disadvantage is that they will become much larger and there will be some efficiency losses from the metal plate not intercepting the entirety of the filler gasses.
Let us assume a 1 kt yield nuclear shaped charge with 85% directivity. We want the gasses arriving to accelerate a tungsten plate to be no hotter than 30000K, as calculated in our example above.
How hot can the initial filler get?
If we use the original 22.5 degree cone, and state that the filler starts out 1m wide (surface area 3.14m^2), then in 10 meters spacing it will have spread out to a disk 5m wide (19.47m^2). This linear expansion would cool the plasma by a factor 6.2. The initial plasma temperature can be 186000 K and allow velocities (186000/4010)^0.5 about 7 times higher than with chemical explosives.
If we increase the spacing to 20 meters, the plasma would cool by a factor 20. The initial plasma temperature can be 602400 K and velocities 12.25 higher.
We could instead reduce the radius of the filler down to 10cm and increase the propellant cone's angle to 45 degrees to achieve an expansion and cooling ratio within 10 meters of 7022, within 20 meters of 27755, allowing velocities 83 and 477 times faster!
Here is a simple equation to determine how the spacing and spread angle cools the plasma and allows for higher projectile velocities, based on the results from the experiment cited above.
Velocity factor = ((tanA * Spacing + Ri) / Ri ) ^ 2 * (Ts / Tc ))^0.5
Velocity factor is how much faster the NEFP projectile can be compared to a chemical EFP. Velocities for chemical EFPs at 2 to 3km/s.
A is half the spread angle. For the Orion drive, this is 11.25 degrees.
Spacing is the distance between the filler and the metal plate, in meters.
Ri is the initial radius of the filler, in meters.
Ts is the survivable temperature of the metal plate. For tungsten, it should be 30000 Kelvin.
Tc is the chemical gas temperature we are using as a reference. For our example, this is 4000 Kelvin.
Using this equation, we determine that a 1kt yield shaped charge with 85% directivity, spreading by 60 degrees (30 degree half-angle), Ri 15cm, and placed 10 meters away from a 16.7kg tungsten plate could reach velocities of up to 324km/s.
The same warhead with the same spread at 25 meters distance would be able to accelerate a 2.75kg plate to 798km/s.
A problem with very high spread angles is that some of the gas particle's kinetic energy is not perpendicular to the plate and therefore does not contribute to its acceleration. Great separation distances increases losses from gasses expanding laterally and not being intercepted by the plate. Overall efficiency would be lower in these cases.
Nuclear HEAT or Nuclear Munroe Projectile
Using the Monroe effect on metal cones angled sharply inwards allows for jets with tip velocities 7 to 10 times greater than the velocity of the explosive gasses driving them.
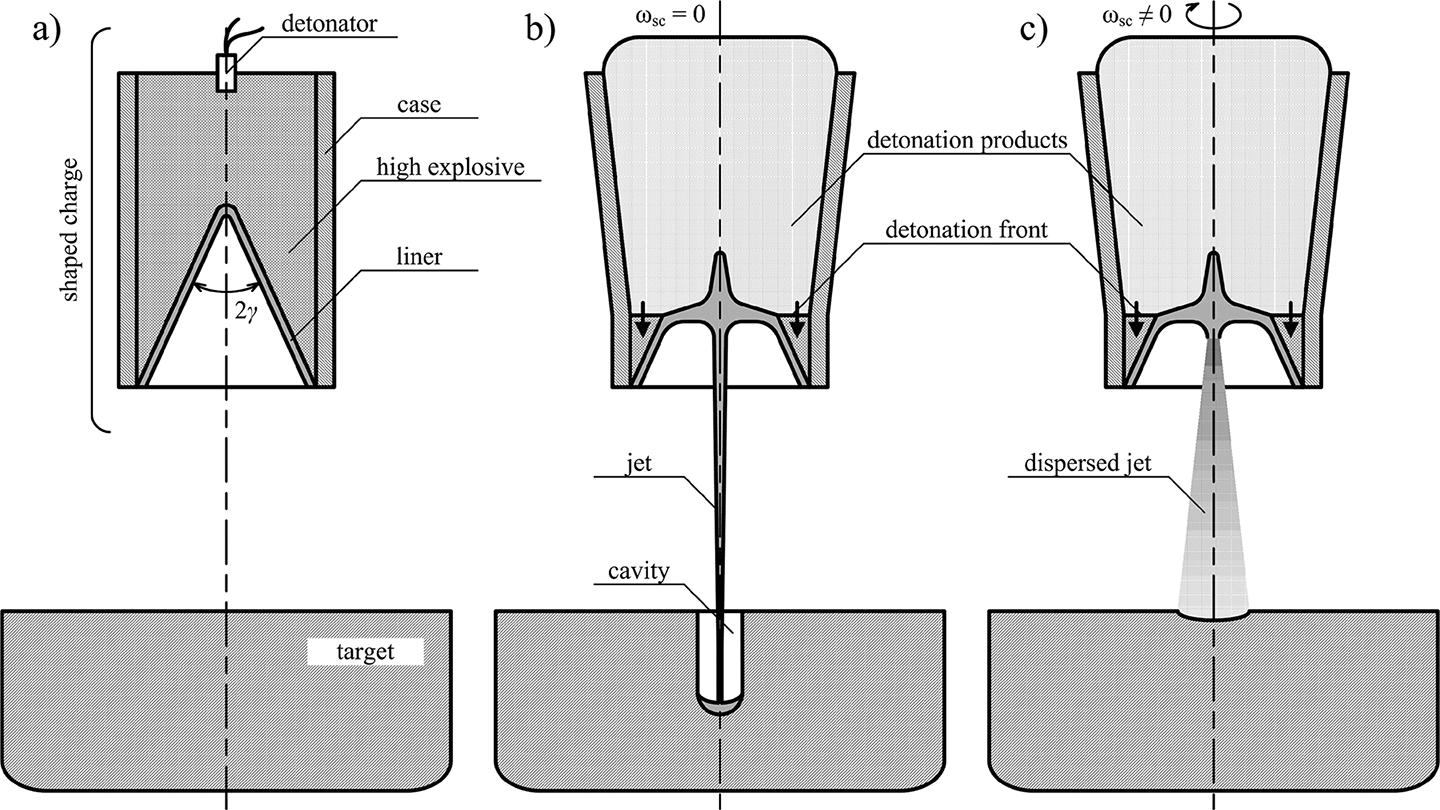
Method of operation
Modern HEAT weapons generate tip velocities of up to 14km/s using gasses that travel no faster than 2 or 3km/s.
A 'Nuclear Monroe Projectile' would therefore produce metal jets of 60 to 90km/s.
If the maximum particle velocity in a fusion shaped charge is 3% of the speed of light, then the Monroe effect can increase this velocity to 30%.
However, there are severe limitations that reduce the effectiveness of this type of weapon.
The first is the standoff distance.

HEAT warhead testing for the correct standoff distance.
While the tip of the jet can reach astounding velocities, the main body of the projectile reaches much lower velocity, with the rearmost 'slug' remaining mostly stationary relative to the warhead.
The large velocity differential stretches out the jet to the point of fragmentation and uselessness. Tip velocities of several tens of kilometers per second would disrupt a jet in milliseconds, meaning that it has to be fired close enough to its target to penetrate with an intact jet.
The standoff distance would be measured in single meters.
The second is efficiency.
In a NEFP, 21% of the nuclear yield ends up as the kinetic energy of the projectile. In a NMP, the kinetic energy is shared between a small fast tip, a slow moving body and a mostly stationary slug concentrating most of the mass. This reduces the overall efficiency of the weapon to a few percent.
In a realistic space setting, getting an intact warhead close to the target before it detonates is a difficult task. In most cases, factors which make this easier (massed missile attacks, high velocity warheads) reduce the usefulness of nuclear warheads (high per-unit costs, waste of missile's kinetic energy).
Performance compared to lasers and Casaba Howitzers
Lasers are generally taken to be low-efficiency, long-ranged weapons which require so many high-mass components that spaceships are built around them. Their extreme effective range can further be extended by relatively cheap methods (larger focusing mirror, laser webs) once the initial investment in radiators, reactors, cooling systems, electrical generators and so on, is made.
Casaba Howitzers unlock the potential of nuclear energy at long distances. Conventional nuclear warheads waste their energy in spherical explosions that cannot harm spaceships beyond a few kilometers. A Casaba Howtizer focuses this nuclear energy into particle beams that can vaporize targets at close range and cover large swathes of space in burning plasma for only a few hundred kilograms per warhead.
At an average 1kW/kg from reactor to radiator through all the components required for a laser weapon, a gigawatt beam would require an investment of 1000 tons.


This 1000 ton weapon would maintain a 10mm/s penetration rate in Aluminium at about 25000km, using a 40m wide mirror and 400nm wavelength.
In comparison, a much less complex spaceship could arms itself with 285 Casaba Howitzers with 10 megaton yield and 0.001 radian directivity, with the 10000km effective range. The lack of huge radiators and power requirements means that some stealth tactics are possible, wherein the spaceship unloads its missiles and overwhelms its targets with multiple particle beams each.
However, if the Casaba Howitzer-equipped spaceship is detected and intercepted, it will lose to the laser. The laser can fire indefinitely and stay outside of the range of the particle beams.
Increase the yield of the nuclear warheads to reduce the range gap quickly reduces the mass advantage they have over a reusable laser. A 150 megaton yield warhead would be effective out to 25000km, but would mass more than 52 tons each.
The solution is the spaced NEFP. Its effective range is practically infinite. A 1 megaton warhead could propel a 2.7 ton projectile to 800km/s, while massing only about 3 tons. This projectile crosses the laser's effective range in about 30 seconds, gouges out a crater nearly a 100 meters deep and/or cracks the target in half with 2160 kN.m of momentum concentrated on a spot less than a meter wide.

